Three Experiments Challenging Einstein’s RelativisticMechanics and Traditional Electromagnetic Acceleration Theory(variant ¹ 2)
www.electrosad.ru | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Abstract
First Experiment: The speed of
electrons accelerated by a Linac was measured in order to clarify
whetherthe Linac’s effective accelerating
force depends upon the speed of electrons or not.
§1 IntroductionAccording to Einstein’s relativistic mechanics, if an object with static mass m0 moves at speed V , then its moving mass is
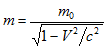
and kinetic energy is Ek =( m – m0) c2. Scientists have done experiments with high-speed electrons to examine these Einsteinian formulas. Most experiments were based on the traditional electromagnetic acceleration theory, which deems the electromagnetic force acting on moving electrons independent of the speed of electrons. Some scientists feel doubtful about it. To check these Einsteinian formulas and the traditional electromagnetic acceleration theory, we have applied high-speed electrons emitted from a linear accelerator (Linac) to do three kinds of experiments: [1][2] (1) To measure the speed of accelerated electrons in order to calculate the kinetic energy gained by the electrons and compare it with the energy spent by the Linac. (2) By use of high-speed electrons to bombard a lead target and to measure the target’s temperature increase due to the kinetic energy of bombarding electrons. (3) To inject high-speed electrons perpendicularly into a homogeneous magnetic field and measure the radius of circular motion of electrons under the action of the Lorentzian deflecting force. All the three experiments were conducted on a femto-second Linac at Shanghai Institute of Applied Physics. The experiments provided clear data to check the traditional electromagnetic acceleration theory and the formulas of moving mass and kinetic energy. Analyzing the data from the three experiments, this paper proves: (1) The actually effective force exerted by an accelerator on moving electrons depends upon the speed V of the electrons. There exists a "c -V phenomenon” (or “wind-sail phenomenon”) so that the higher the electron’s speed V , the less efficient the Linac is. Traditional electromagnetic acceleration theory is incorrect . The endless pursuit of accelerator’s power, including the construction of the costly European Large Hadron Collider (LHC), is a meaningless waste of money. (2) In a homogeneous magnetic field, the effectiveness of the Lorentzian deflecting force, which acts on moving electrons, depends upon the speed V of electrons. There also exists a "c -V phenomenon” and it is necessary to introduce a coefficient to match theoretical and experimental data. (3) The results from all the three experiments do not accord with Einstein’s formulas of moving mass and kinetic energy, but conform with the formulas in the New electrodynamics of moving bodies [3][4] ,
§2 Experiment on the Acceleration of Electrons in a Homogeneous Electric Field§2.1 Method and Results of the ExperimentThe front of electrons emitted from a Linac continues its linear and uniform motion through a straight tube with length of S 1.43[m]. Sensors were installed at both ends of a section of the tube to measure the entry time t1 and the exit time t2 of the electronic front into and out of the section. The speed gained by electrons due to the Linac’s acceleration was calculated as V = S/(t2 – t1) The experimental results are shown in Table 1: Òàble 1
§2.2 AnalysisFrom Einstein’s
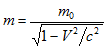
and Ek =( m – m0) c2 , we have
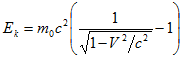
so that, having measured speed V , we can calculate the kinetic energy Ek gained by the electrons and the efficiency of the Linac as Åk/E
Òàble 2
It is surprisingly strange that the kinetic energies of accelerated electrons are more than the Linac can give them and the Linac’s efficiencies are more than 100%! Obviously, both the Einsteinian relativistic mechanics and the traditional electromagnetic acceleration theory are questionable. In accordance with the New electrodynamics of moving bodies [3][4] , which is based solely on Galilean principle of relativity without Einstein’s postulate of the constant speed of light and Loretnz’s postulate of the length-contraction, if a static body (V 0 ) is accelerated to the speed of Vthen it obtains the kinetic energy Ek = mV2/2. On this formula we can get following results
Òàble 3
As the speed of the electrons increases, the Linac’s efficiency decreases. This is understandable because the electromagnetic force cannot push electrons to reach the speed of light c which is the speed of electromagnetic action. This is similar to the case between wind-force and sailing-boat: A sailing-boat’s speed can never be equal to the wind’s speed. Because, as the boat’s speed approaches the wind’s speed, the wind’s effective force acting on the boat’s sail reduces sharply. A great amount of the windpower is wasted. In case of the electromagnetic acceleration, let’s call it a “c -V phenomenon”.
§3 Calorimetric Experiment with High-Speed Electrons Bombarding a Lead Target§3.1 Method and Results of the ExperimentHigh-speed electrons from a Linac bombarded a lead target. The Linac’s working energy levels were set up at 6 MeV, 8MeV, 10MeV, 12MeV and 15MeV. The current strength of electrons was 1.26A with the impulse width of 5[ns] and frequency 5[Hz]. The electrons bombarded the target for 120[s], So, each bombardment’s cumulative time was only 120x 5x 10-9 x5 =3x 10-6 [s]. The cumulative electric charges receiveed by the target was 1.26x 3x 10-6 = 3.78x 10-6 [Coulomb]. Since 1[Coulomb] 6.2415x1018 electrons, so the target received 3.78x10-6 x6.2415x1018 2.36x1013 electrons. Since 1 [MeV] 1,602õ10-13[Joule], so each 1MeV of the 2,36õ1013 electrons is equivalent to 2,36õ1013õ1,6021733õ10-13=3,78 [Joule]. The target’s mass is 70[g]. Since the lead’s specific heat is 13 [J/g ⋅°C], so 70 õ0.13 9.1[Joule] is needed for the lead target’s temperature to increase 1°C . The temperature is measured by a thermoelectric couple. The experiment’s equipment and the measured values of the lead target’s temperature increase are shown below:
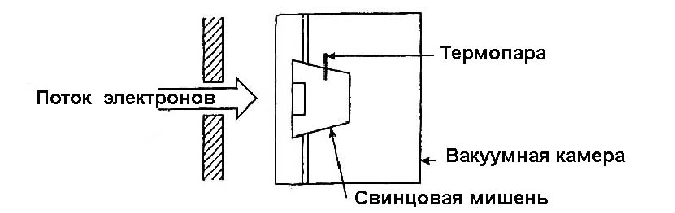 Òàble 4
The target’s temperature varies very little, although the
Linac’s working energy level changes widely. §3.2 AnalysisThe traditional theory of electromagnetic acceleration maintains that the actually effective force exerted by an accelerator on an electron is independent of the electron’s speed and all the accelerator’s working energy E becomes the electron’s kinetic energy Ek , i.e., E k . If the electrons have actually received all the Linac’s working energy ( E k ), then by use of the Einsteinian formula:
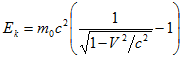
their speeds can be calculated as:
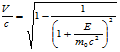
The kinetic energy E k of electrons causes the increase of the lead target’s temperature. The increase of temperature can be calculated as
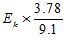 °C °C
Given E k and by use of Einstein’s (3.1) , the calculated values of the lead target’s temperature increase are:
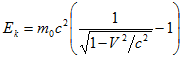
On the other hand, the Linac’s efficiency decreases sharply as the speed of electrons approaches the speed of light (i.e., the “ c -V phenomenon” shown in §2) so that the electrons did not reach the speed as high as above calculated in the Table 5. Let’s take the “ c -V phenomenon” into consideration. An accelerator’s work is to make its electromagnetic field’s potential energy to become the electron’s kinetic energy, i.e., to change the Linac’s potential head into electron’s velocity head: Fdx mvdv. In the New electrodynamics of moving bodies is shown that when moving the charge along field efficient power F can be denominated F=F0(1-V2/c2) where V is the electron’s speed and F0 is the accelerator’s nominal force of action. With provision for always existing when working the physical installing the losses to energ we have
F=F0(1- δ - V2/c2)dx=mvdv or 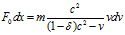
The nominal work done by an accelerator consuming energy E is ∫F0dx E, which accelerates an electron from υ 0 to υ = V
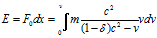 (3.2) (3.2)
After integrating we get:
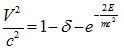 (3.3)
(3.3)
By use of (3.3) we can calculate the actual speed V of the electrons accelerated by the Linac’s certain working energy E and consequently their kinetic energy, The known [5] that in linear booster electrons by leaps and bounds, at energy 1-3 Mev, take the velocity close to velocities of the light. Degree of the approximation to velocities of the light is defined loss to energy electron in booster and, what follows from experiment on deflection electron to high energy in uniform magnetic field, forms value 0,997ñ. With provision for that full energy electron stands out on dartboard we can also calculate the lead target’s actual temperature increase as (Ek+mc2 )õ3,78/9.1[°C],the Linac’s wasted energy ΔE = E – Ek and its efficiency Åk/E
Òàble 6
The calculated values of the lead target’s temperature increase vary little and match the varying trend of the measured values in the Table 4. Obviously, the classical mechanics together with the consideration of the "c -V phenomenon” can explain why the lead target’s temperature increases so little.
§4 Experiment on the Deflection of High-Speed Electrons in a Homogeneous Magnetic Field§4.1 Method and Results of the ExperimentA stream of high-speed electrons from a Linac is perpendicularly injected through a rectilinear correcting tube made of 10cm thick lead-iron combination into a chamber with homogeneous magnetic field. To avoid any outside electromagnetic interference, the magnetic field is created by a permanent magnet, not by an electromagnet. The gap between two poles of the magnet is as narrow as just 2.5[cm] in order to make the magnetic field between the two poles as homogeneous as possible. Three series of experiments were done with three magnets of 0.121[tesla], 0.081[tesla] and 0.063[tesla] respectively. The Linac’s working energy levels were set up at 4MeV, 6MeV, 9MeV, 12 MeV, 16MeV and 20 MeV. The experiment’s equipment is shown below:
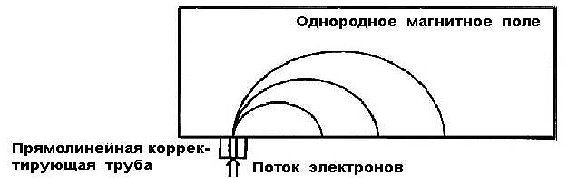
Òàble 7
The measured values of radius R for the Linac’s six different energy levels remain almost constant. The six small sesame-size spots merged together and appeared on the screen as a single big bean-size spot with its width of about 0.5[cm] so that there are about R ≈17.75 [cm], 26.75 [cm], 34.75[cm] at the low energy end of E 4 [Mev] and R ≈18.25 [cm], 27.25[cm], 35.25[cm] at the high energy end of E 20 [Mev]. §4.2 AnalysisTraditional theory deems that the Lorentz force, which deflects an electron moving in a static homogeneous magnetic field, is irrelevant to the electron’s speed V . If the strength of a static homogeneous magnetic field isB , then the theoretical Lorentz deflecting force is F0 eVB. The Lorentz deflecting force is balanced by the centrifugal force acting on an electron moving circularly due to the deflection. Therefore, the kinematic equation of the electron’s circular motion is: mV2/R = eVB or R = mV/ eB , [4.1]
where m is the electron’s moving mass and R is the radius of the electron’s circular track. Einstein’s formula
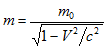
makes the equation (4.1) becoming:
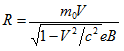
or
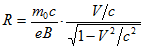 [4.2] [4.2]The traditional electromagnetic acceleration theory maintains that all the Linac’s working energy E istransferred to the accelerated electron and becomes the electron’s kinetuic energy k E so that E E k . Asabove-mentioned in §3.2, the traditional electromagnetic acceleration theory and the Einsteinian relativisticmechanics together lead to the formula (3.1). By use of (3.1) we can calculate the electron’s speed V andthen by use of (4.2) we can calculate the radius R of the electron’s circular motion. The calculated values ofR are shown below:
Òàble 8
The above-mentioned calorimetric experiment with high-speed electrons bombarding a lead target has revealed a "c -V phenomenon” (see §3.2). By use of the formula (3.3), which takes the "c -V phenomenon” into consideration, we can calculate the speed V of electrons entering the magnetic field from the Linac. On the other hand, in the New electrodynamics of moving bodies [3][4] is shown that when moving the charge in transverse magnetic field dependency interactions of the charge exists with field from its velocities under the law:
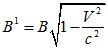
Considering this phenomena in (4,1) we get complying with (4.2) formula:
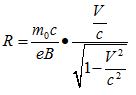 (4.3
) (4.3
)
With provision for this on formula (4.3) we can calculate radius R :
§5 Questioning European Large Hadron Collider (LHC)It was reported that the world’s most powerful collider—European LHC succeeded in accelerating protons to the energy level of 3.5[Tev] and protons had obtained speed of V ≈ 0.99999995c Obviously, CERN’s scientists stick to Einstein’s relativistic mechanics and traditional electromagnetic acceleration theory in the calculation of the speed of their protons. Indeed, according to the formula (3.1), which comes from Einstein’srelativistic mechanics and assumes the electromagmetic acceleration is 100% efficient, if E = 3.5[Tev], then V ≈ 0.99999995c which is only 15 > ms less than the speed of light. CERN’s scientists believe that, with V ≈ 0.99999995c, each proton has huge moving mass
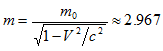 Òev Òev[ Òev ] and kinetic energy Ek= 3,5[Òev]. The cumulative energy of two colliding protons is 2E=7[Òev]. The collision speed is - 0.9999999999995C according to Einstein’s law of addition of speeds. The collision may lead to some new physical findings mainly due to proton’s huge moving mass with huge energy. However according to our formula (3.3), which is founded on classical mechanics and takes the "c -V phenomenon” into consideration, the protons were speed before smaller velocities. Moreover if even proton moves at the speed of C he possesses the kinetic energy, equal only 469,13 [MeV], far less than the LHC’s energy E = 3.5[Tev]. The LHC’s efficiency is only about 0.013%
With V increasing, the acceleration becomes less and less efficient because of the "c -V phenomenon”. It is not because a particle’s moving mass drastically increases as its speed approaches c , according to Einstein’s relativistic mechanics, so that the acceleration becomes harder and harder. Nevertheless, according to the Galilean law of addition of speeds, the collision speed is high:
V + V =(2- δ) C ≈2C.
The collision may lead to some new physical findings mainly because of the huge collision speed, not due to proton’s moving mass and kinetic energy which remain small. CERN is going to double its LHC’s power to [Tev] to accelerate protons to V = 0.999999991c (only about 12.3 m/s higher than in case of LHC’s energy E = 3.5 [Tev] and only 2.7m/s less than the speed of light) so that Vsum~ C, m ≈ ∞ è Ek≈ ∞. Mainstream scientists guess such collisions may cause a Big Bang and help them to know some scenario at the Birth of Universe. However, according to our formula (3.3), LHC’s 7 [Tev] energy can only accelerate protons to
V≈(1- δ/2) C
The results are almost the same as those in case of LHC’s energy E 3.5[Tev]. This is because the “ c -V phenomenon” lowers LHC’s efficiency further down to 0.0065% The collision speed is
V + V = 2(1-δ/2) C ≈ 2C.
No matter how powerful a collider is, the collision speed will always be less than 2c. Disregarding the "c -V phenomenon”, the costly LHC has been wasting a great amount of energy and money to do ineffective work. Indeed, what CERN ought to do is not to double the LHC’s power but to increase the current density of its proton stream. Because, not any kind of collision of two protons may cause new physical phenomena. Oblique collisions are ineffective. Only precise head-on collisions, the probability of which is extremely small, are effective and deadly needed for finding new physical phenomena. Yet, with LHC’s energy 7 [Tev], the total kinetic energy of two precisely head-on colliding protons is only
2Ek≈ 938,26 [ Ìev]
There won’t be any Big Bang or Birth of Universe.
§6 Conclusions(1) All the three experiments prove that the traditional electromagnetic acceleration theory and Einstein’s relativistic mechanics are misleading. Electromagnetic acceleration cannot push a charged particle to V ≈c. It is not because a particle’s moving mass drastically increases as its speed approaches c so that the acceleration becomes harder and harder. It is because the "c -V phenomenon” makes the acceleration less and less efficient. (2) Einstein’s relativistic mechanics can not explain the results from all the three experiments but the Classical mechanics with the New electrodynamics of moving bodies can. (3) The Lorentzian deflecting force, which stems from the interaction between a static magnetic field and a moving electron’s moving magnetic field, depends upon the speed of the moving electron. (4) In order to examine the "c -V phenomenon” we suggest physicists to repeat these experiments more accurately and by use of more wide speed electrons.
Literature[1] Ji Hao, “Calorimetric Experiment to Test the Mass-Speed Relationship”, China Sci-Tech Achievements, 2009(1) [2] Ji Hao, “Experiment on the Motion of Electrons in a Homogeneous Magnetic Field”, China Sci-Tech Length and Breadth,2009(6) [3] Ñ.Í.Ïóõîâ, “Íîâàÿ ýëåêòðîäèíàìèêà äâèæóùèõñÿ òåë “, Äåï. â ÂÈÍÈÒÈ 9,06,1993ã.,N1582-B93. [4] Ñ.Í.Ïóõîâ, “Íîâàÿ ýëåêòðîäèíàìèêà äâèæóùèõñÿ òåë “, Âëàäèìèð, 1994ã. [5] Å.Ã.Êîìàð, “Îñíîâû óñêîðèòåëüíîé òåõíèêè“, ñ.349,Ì., Àòîìèçäàò, 1975ã.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ïîïàñòü ïðÿìî â ðàçäåëû ñàéòà ìîæíî çäåñü:
/Íåèçâåñòíûé
ïðîöåññîð/Îõëàæäåíèå ÏÊ/Ýëåêòðîíèêà äëÿ ÏÊ/Linux/Ïðîåêòû, èäåè/Ïîëåçíûå ñîâåòû/Ðàçíîå/
Ïðè ïîëíîì èëè ÷àñòè÷íîì èñïîëüçîâàíèè ìàòåðèàëîâ ññûëêà íà "www.electrosad.ru" îáÿçàòåëüíà. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Copyright © Sorokin A.D. |
|
2002 - 2020 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||